Year: 2022
원문: https://arxiv.org/abs/2110.02861
저자: Facebook AI Research
GitHub - TimDettmers/bitsandbytes: Accessible large language models via k-bit quantization for PyTorch.
Accessible large language models via k-bit quantization for PyTorch. - TimDettmers/bitsandbytes
github.com
- 모델 크기를 늘리는것은 리소스에 대해 더 나은 성능을 달성하는 방법입니다. (Scaling Laws for Neural Language Models 논문 참고)
- 이런 대규모 모델을 학습하려면 model, gradient, state of the optimizer를 사용가능한 양의 메모리에 저장해야합니다.
- 기존은 모델 파라미터에 필요한 메모리를 줄이거나 분산하여 큰 모델을 학습하는데 중점을 두었습니다.
- state of the optimizer는 학습 중 메모리 공간의 33-75%를 차지하는데 이를 줄이는 연구는 덜 연구 되었습니다.
- 예를들어 gpt2 및 t5 모델의 Adam의 메모리 소모량은 11gb, 41gb입니다.
- 여기서는 기존의 하이퍼 파라미터를 변경하지 않고 일부메모리 공간을 사용해 32비트 성능을 유지하는 8-bit optimizer를 가능하게 하는 방식(fast, high-precision non-linear quantization method – block-wise dynamic quantization)을 소개합니다.
1B이상의 파라미터가 있는 대규모 모델에서는 16비트 optimizer를 사용하기 힘들었습니다.(Zero-shot text-to-image generation 논문 참고). 16비트 optimizer에서 8-bit optimizer로 전환하면 범위가 $2^{16}=65536$ 에서 $2^8=256$으로 줄어들기때문입니다.
이 제한된 범위를 사용하는건 quantization accuracy, computational efficiency, and large-scale stability (양자화 정확도, 계산 효율성, 안정성) 때문에 어렵습니다.
정확도를 유지하려면 일반적인 작은 크기 값과 가끔 나오는 큰 값(이상치로 해석됨) 모두에 대한 오류를 줄이기 위해 일종의 비선형 양자화를 도입하는 것이 중요합니다.
그런데 8비트 optimizer는 훈련속도를 늦추지 않을 만큼 빨라야 하고, quantization bucket을 유지하기 위해 더 복잡한 데이터 구조가 필요한 비선형 방법의 경우 더 어렵습니다.
마지막으로 1B 파라미터를 초과하는 대규모 모델에 대한 안정성을 유지하기 위해 good mean error만 가지면 안되고 excellent worse case에도 성능이 좋아야 합니다. single large quantization 오차가 전체 훈련 과정을 발산할 수 있기 때문입니다.

Figure 1:
Quantization
optimizer 업데이트가 32비트로 수행 → state tensor는 block으로 청크(작은 블록으로 나누어 처리)→ 각 블록의 절대 최대값으로 정규화 → 동적양자화 수행 → 인덱스 저장
Dequantization
인덱스 조회 → 블록 단위 절대 최대값과 곱하여 후속 비 정규화 → 이상치는 블록 단위 양자화를 통해 단일 블록으로 제한
이런 세 가지 문제(quantization accuracy, computational efficiency, and large-scale stability를 모두 해결하는 Block-wise quantization 접근 방식을 도입합니다.
Block-wise quantization
input tensor를 Block으로 분할하고 각 Block에서 독립적인 quantization을 수행
⇒ Block별 분할은 이상치가 특정 블록으로 isolated되기 때문에 quantization 프로세스에 대한 이상치의 영향을 줄여 대규모 모델의 안정성과 성능을 향상시킵니다.
Block단위 처리는 각 정규화(norm)가 각 코어에서 독립적으로 계산될 수 있기 때문에 높은 optimizer 처리량을 허용하고, task core scheduling에 의존하는 slow cross-core synchronization가 필요한 tensor 전체 정규화와 대조됩니다.
Block-wise quantization는 8bit optimizer를 위해 dynamic quantization 와 stable embedding layer을 결합합니다.
dynamic quantization: 부호 없는 입력 데이터에 대한 dynamic tree quantization의 확장
stable embedding layer: 극단적인 gradient 변동을 피하기 위해 정규화
1 BACKGROUND
1.1 STATEFUL OPTIMIZERS

where $\beta1$ and $\beta2$ are smoothing constants, $\epsilon$ is a small constant, and α is the learning rate.
32bit의 경우 Momentum 및 Adam은 파라미터당 4바이트 및 8바이트 즉 1B 파라미터 모델의 경우 4GB, 8GB인데 8bit non-linear quantization은 1GB, 2GB로 줄입니다.
1.2 NON-LINEAR QUANTIZATION
quantization은 정밀도를 희생하는 대신 공간을 절약하기 위해 숫자 표현을 압축합니다
quantization은 k-bit 정수를 D의 실제 요소, 즉 $Q^{map}:[0, 2^k-1] \mapsto D$로 매핑 됩니다.
For example, 32-bit floating data type은 인덱스 $0…2^{32}-1$을 도메인 [-3.4e38, +3.4e38]에 매핑합니다.
notation: $Q^{map}(i) = Q_i^{map}=q_i$ (e.g., $Q^{map}(2^{31}+131072)=2.03125$
한 데이터 유형에서 다른 데이터 유형으로 일반적인 양자화를 하려면 세 단계가 필요합니다.
- 입력 Tensor T를 대상 target quantization data type $Q^{map}$의 영역 D 범위로 변환하는 정규화 상수 N 계산
- T/N의 각 요소에 대해 도메인 D에서 가장 가까운 대응값 $q_i$를 찾기
- 양자화된 output Tensor $T^Q$d에 $q_i$에 해당하는 index $i$를 저장
dequantized된 Tensor $T^D$를 receive하기 위해 index를 조회하고 denormalize 합니다.
$T^D_i=Q^{map}(T^Q_i)·N$
dynamic quantization를 위해 이 절차를 수행하려면 먼저 절대 최대값으로 나누기를 통해 [-1, 1]범위로 정규화 합니다 $N = max(|T|).$
그런 다음 binary search를 통해 가장 가까운 값(closest values)을 찾습니다.
$$
\mathbf{T}_i^Q=\underset{j=0}{2^n} \operatorname{\operatorname {arg}\operatorname {min}}\left|\mathbf{Q}_j^{\text {map }}-\frac{\mathbf{T}_i}{N}\right|
$$
1.3 DYNAMIC TREE QUANTIZATION

Dynamic Tree quantization는 크고 작은 값에 대해 낮은 quantization error를 생성하는 방법입니다.
고정 지수 및 분수가 있는 데이터 유형과 달리 Dynamic Tree quantization는 각 숫자에 따라 변경될 수 있는 동적 지수 및 분수가 있는 데이터 유형을 사용합니다
그림 2 같이 네 부분으로 구성됩니다.
(1) 데이터 유형의 첫 번째 비트는 부호용으로 예약되어 있습니다.
(2) 연속된 0 비트의 수는 지수의 크기를 나타냅니다.
(3) 1로 설정된 첫 번째 비트는 다음 값이 모두
(4) 선형 양자화를 위해 예약되어 있음을 나타냅니다.
indicator bit 를 이동하면 숫자는 $10^{-7}$의 큰 지수 또는 1/63의 높은 정밀도를 가질 수 있습니다. 선형 양자화와 비교할 때 동적 트리 양자화는 균일하지 않은 분포에 대해 더 나은 absolute and relative quantization errors를 가지고 있습니다. 동적 트리 양자화는 [-1.0, 1.0] 범위의 숫자를 양자화하도록 엄격하게 정의되며, 이는 텐서 수준의 absolute max normalization를 수행하여 보장됩니다.
2 8-BIT OPTIMIZERS
8-bit optimizers have three components
(1) Block-wise quantization
입력 텐서를 작은 블록으로 나누고 각 블록을 독립적으로 양자화합니다. 이렇게 하면 이상치(outliers)가 특정 블록에 국한되어 전체 양자화 과정에서의 오류 분포가 더 균일해집니다
(2) Dynamic quantization
크고 작은 수치 모두를 높은 정밀도로 양자화할 수 있게 해줍니다. 이는 비선형 최적화 형태로, 각 수치의 크기에 따라 양자화 정밀도가 달라집니다.
(3) Stable embedding layer
이 레이어는 단어 임베딩을 포함한 모델에서 최적화 과정 중 안정성을 개선하기 위해 설계되었습니다. 이는 입력 토큰의 분포가 매우 비균일할 때 발생할 수 있는 그래디언트의 변동을 줄이는 데 도움을 줍니다.
2.1 BLOCK-WISE QUANTIZATION
- 입력 텐서 분할: 입력 텐서 𝑇를 1차원 요소 시퀀스로 처리하고, 이를 크기 𝐵의 블록으로 나눕니다. 예를 들어, 텐서 𝑇가 𝑛개의 요소를 가지고 있다면, 𝑛/𝐵 개의 블록이 생성됩니다.
- 블록별 정규화: 각 블록 𝑏에 대해 최대 절대값 $max(∣𝑇𝑏∣)$을 계산하여 블록별 정규화 상수 $N_b$를 결정합니다. 이는 각 블록의 모든 값을 [−1,1]범위로 조정하는 데 사용됩니다.
- 독립적 양자화: 정규화된 각 블록은 독립적으로 양자화됩니다. 정규화 상수$N_b$를 사용하여 각 블록 내의 값을 상대적으로 스케일링하고, 이 스케일된 값에 대해 8비트 등의 낮은 비트 양자화를 적용합니다.
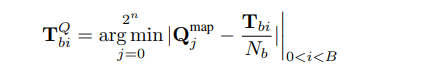
- 이 접근 방식은 안정성 과 효율성 측면에서 여러 가지 장점을갖고 있습니다 .
- 첫째, 각 블록 정규화는 독립적으로 계산될 수 있습니다. 따라서 코어 간 동기화가 필요하지 않으며 처리량이 향상됩니다.
- 둘째, 입력 텐서의 이상치에 대해 훨씬 더 강력합니다.
2.2 DYNAMIC QUANTIZATION
- 두 번째 Adam 상태는 엄격히 양수이므로이 작업에서는 부호 비트를 다시 용도 지정하여 부호 없는 입력 텐서에 대해 동적 트리 양자화를 확장합니다 .
- 동적 트리 양자화는 분수에 대한 고정 비트로 확장됩니다. 이 확장은 두 번째 Adam 상태가 언어 모델 훈련 중에 약 3~5배 정도 변한다는 관찰에 의해 동기가 부여되었습니다 . 이에 비해 동적 트리 양자화는 이미 7차수 범위를 갖습니다.
2.3 STABLE EMBEDDING LAYER
NLP 작업에 대한 안정적인 학습을 보장하도록 설계된 표준 단어 임베딩 레이어 변형(Devlin et al., 2019)입니다. 이 임베딩 레이어는 extreme gradient variation을 피하기 위해 normalizing the highly non-uniform distribution하여 보다 aggressive quantization를 지원합니다
위치 임베딩을 추가하기 전에 Xavier 균일 초기화(Glorot and Bengio, 2010)로 Stable Embedding Layer를 초기화하고 layer normalization을 적용합니다. 초기화 시와 훈련 중에 약 1의 분산을 유지합니다. 또한, uniform distribution initialization은 정규분포보다 극단값이 적기 때문에 최대 기울기 크기가 줄어듭니다.
3 8-BIT VS 32-BIT OPTIMIZER PERFORMANCE FOR COMMON BENCHMARKS
Experimental Setup
Adam, AdamW, Momentum을 사용하여 실험하였습니다.
32-bit optimizer를 8-bit optimizer로 변경만 하였으며, 학습 시 16-bit mixed-precision을 사용하였습니다.
Result

제안된 8비트 최적화 프로그램은 최대 1.5B 매개변수 언어 모델의 경우 최대 8.5GB의 GPU 메모리를 절약 하고 RoBERTa 의 경우 2.0GB를 절약합니다 .
Ablation Analysis
The runs without dynamic quantization use linear quantization
dynamic quantization는 일반적인 안정성에 중요하고 block-wise quantization는 대규모 안정성에 중요하다는 것을 알 수 있습니다
stable embedding layesms 8, 32-bit 모두에 유용하며 안정성을 어느 정도 향상시킵니다.
We use the hyperparameters $\epsilon$ {1e-8, 1e-7, 1e-6}, $\beta1$ {0.90, 0.87, 0.93}, $\beta2$ {0.999, 0.99, 0.98} and small changes in learning rates
dynamic quantization, block-wise quantization, and the stable embedding layer가 성능 또는 안정성에 중요하다는 것을 보여줍니다. 또한 block-wise quantization는 대규모 언어 모델 안정성에 매우 중요합니다.

Sensitivity Analysis

8bit와 32bit Adam사이에 비교적 일정한 간격이 있음을 보여주며, 이는 8bit Adam이 32bit Adam에 비해 추가 하이퍼파라미터 튜닝이 필요하지 않음을 시사합니다.
LIMITATION
자연어 작업을 위한 8-bit optimizer가 32-bit 성능으로 훈련되기 위해 STABILITY OF EMBEDDING LAYERS가 필요하다는 것입니다. 8-bit optimizer는 파라미터 개수에 비례하여 메모리 공간만 줄이므로, 컨벌루션 신경망과 같이 많은 양의 활성화 메모리를 사용하는 모델은 8-bit optimizer를 사용해도 얻을 수 있는 이점이 거의 없습니다. 따라서 88-bit optimizer는 메모리 제약이 심한 GPU에서 파라미터가 많은 모델을 훈련시키거나 미세 조정하는 데 가장 유용합니다
Appendix
Stable embedding layer
Word embedding layer 주된 불안정성은 그것이 희소(sparse) layer며 입력이 비균일하게 분포되어 있기 때문에 발생합니다. 이는 일부 토큰에 대해 다른 layer최대 100배 큰 gradient 크기를 생성할 수 있습니다. 대부분의 딥러닝 프레임워크는 미니 배치 내의 총 토큰 수에 따라 gradient 를 정규화하지만, 각각의 토큰 빈도에 따라서는 정규화하지 않습니다. 이로 인해 특정 토큰의 gradient 크기가 배치 크기나 배치 간에 크게 달라질 수 있습니다. 이를 해결하기 위해 Stable embedding layer를 사용합니다.
Stable embedding layer에는 세 가지 기능이 있습니다.
초기화: Xavier uniform initialization를 활용하여 일관된 분산을 유지하고 큰 기울기의 가능성을 줄입니다.\
def reset_parameters(self):
torch.nn.init.xavier_uniform_(self.weight)
self._fill_padding_idx_with_zero()정규화: position embedding을 추가하기 전에 레이어 정규화를 통합하여 출력 안정성을 돕습니다.
self.norm = torch.nn.LayerNorm(embedding_dim, device=device)
def forward(self, input):
...
return self.norm(emb).to(self.weight.dtype)최적화 상태: 안정성을 향상시키기 위해 이 Layer에만 32bit 최적화 상태를 사용하는 반면, 모델의 나머지 부분은 표준 16bit 정밀도를 사용할 수 있습니다.
GlobalOptimManager.get_instance().register_module_override(self, "weight", {"optim_bits": 32})